Vitor Meriat
Machine Learning EngineerQuantum Computing

A computação quântica é uma área que tem o potencial de revolucionar o campo da computação. O nascimento da mecânica quântica no início do século XX teve profundas implicação em diversas áreas da ciência e influenciou a computação com a descoberta de que computadores baseados em fenômenos quânticos, ou computadores quânticos, eram capazes de realizar cálculos considerados intratáveis na computação clássica. Estre trabalho propõe fornecer uma introdução ao assunto, expondo os fundamentos da mecânica quântica relevantes, descrevendo como seria a arquitetura de um computador quântico e suas propriedades1. Também descrevem-se algoritmo quânticos capazes de uma performance maior comparada a seus equivalentes clássicos.
Sumário
- 1. Introdução
- 2. Computação Quântica
- 3. Bit quântico (q-bit)
- 4. Portas quânticas
- 5. Conclusão
- 6. Referências
1. Introdução
Nos últimos 50 anos, os computadores deixaram de ser do tamanho de salas e deixaram de ser objetos apenas de empresas e privilegiados para estarem à mão de todos, cada vez mais potentes e compactos. Em parte, esta transformação foi possível graças à miniaturização dramática dos componentes básicos de um computador. Esta tendência foi identificada e junto com ela as limitações de ordem física.
Quase concomitante ao desenvolvimento da eletrônica, desencadeadora da construção de computadores, desenvolveu-se, também, a física moderna, onde se afere que sistemas físicos como átomos e partículas de menores grandezas, comportam-se de maneiras muito diferente de objetos do dia a dia. Na verdade, eles são governados pelas leis da mecânica quântica em vez de mecânica clássica.
No início dos anos 80, alguns estudiosos da área começaram a questionar o que significaria um computador operar na escala de um átomo por bit. As operações elementares de tal computador precisariam ser descritas em termos da mecânica quântica.
Físicos e cientistas da computação entenderam que certos efeitos quânticos permitem tipos inteiramente novos de tarefas a serem executadas. Nasce aí um novo paradigma na tecnologia, uma nova área que envolve a matemática, a ciência da computação, a física moderna e engenharias correlatas.
A respeito da rapidez no desenvolvimento do computador clássico, o computador quântico poderá não demorar muito a ser realidade tangível a todos, por isso é necessária a compreensão de que divulgação dessa nova área é o desafio atual.
Este texto contém reflexões sobre Computação Clássica e Computação Quântica. É feita uma análise sobre os computadores que possuímos atualmente, as suas limitações e as possibilidades para o futuro. São apresentados alguns conceitos básicos sobre a Arquitetura de Von Neumann e a Computação Quântica. O enfoque do texto é sobre a significância desses conceitos e as consequências que eles implicam na Ciência da Computação.
1.1. Computação Clássica
O computador tal qual o conhecemos atualmente é baseado na arquitetura de Von Neumann. Um computador de Von Neumann faz uma distinção clara entre elementos de processamento e armazenamento de informações, isto é, possui processador e memória separados por um barramento de comunicação. Mais especificamente, destaca-se duas características em particular sobre um computador de Von Neumann: a organização da memória e o método de processamento. As palavras de memória podem conter tanto instruções como dados. O processamento, por sua vez, é sequencial, podendo conter desvios condicionais ou incondicionais. O reflexo dessas características nos computadores que temos na prática é a existência do program counter (que é incrementado a cada instrução) e da memória principal (que contém os programas executáveis e seus arquivos de dados). Essas são as duas características mais importantes da arquitetura de Von Neumann; elas definem não apenas o computador em si, mas tudo o que está associado com ele, ou seja, desde os algoritmos que são elaborados até a eficiência com que conseguimos resolver determinados problemas.
Para ilustrar melhor a importância dessas características da arquitetura de Von Neumann, considere o exemplo a seguir. Quando um programador implementa um software, computacionalmente, ele está escrevendo um algoritmo para solucionar determinado problema. A forma como a maioria dos programadores pensa e imagina essa solução é de forma sequencial, não apenas porque pensamos de forma sequencial, mas porque os computadores que construímos e utilizamos há cinquenta anos também trabalham de forma sequencial. A programação (estruturada, lógica ou funcional) e o processamento sequencial são consequências diretas da arquitetura de Von Neumann. Mesmo novos paradigmas de programação, como a Orientação a Objetos, ainda estão restritos a Von Neumann.
Essa forma de organizar o computador, apesar de impor algumas restrições, é extremamente eficiente para a maioria das aplicações de um computador moderno. Provavelmente não existe forma melhor de realizar cálculos matemáticos, editar textos, armazenar bancos de dados ou acessar a Internet; um computador de Von Neumann é a melhor máquina para executar essas tarefas. Entretanto, para algumas áreas específicas, como a Inteligência Artificial por exemplo, talvez seja necessário um novo instrumento computacional. De fato, os programas de Inteligência Artificial mais avançados do mundo estão muito longe de alcançar algo semelhante à inteligência humana.
Entretanto, a culpa por não se conseguir uma inteligência artificial de alto nível não pode ser atribuída somente ao hardware. O problema da IA pode ser tanto de software como de hardware. Não se pode afirmar que não existem programas ou máquinas inteligentes porque os computadores atuais não têm potência ou velocidade de processamento suficientes para suportar uma IA avançada. O problema pode ser a nossa falta de conhecimento (ou criatividade) para elaborar os algoritmos necessários. Assim, os processadores atuais podem ser até mais que suficientes para executar uma inteligência artificial ao nível da inteligência humana; nós é que não sabemos ainda como implementar os algoritmos. Por outro lado, a ausência desses algoritmos pode ser uma consequência da falta de computadores suficientemente poderosos. O fato é que não sabemos onde está o problema: no hardware, no software ou em ambos.
1.2 Desafios de Hilbert
Em 1900, em uma palestra intitulada “Mathematische Probleme”, antes do segundo congresso internacional de matemáticos realizado em Paris, David Hilbert (1862 – 1943), profundamente envolvido com os fundamentos da matemática e com a possibilidade teórica de soluções por meios mecânicos, postulou 23 problemas de temas diversos em matemática e áreas afins para serem resolvidos no século XX. O “décimo problema” é sobre equações Diofantinas, conhecido como o problema de decisão, ou “Entscheidungsproblem”.
“Dada uma equação Diofantina, com coeficientes inteiros com um número qualquer de variáveis, é possível elaborar um processo que decida, através de um número finito de operações, se a equação tem soluções inteiras.” 2.
Hoje a expressão “conceber um processo” tem um sentido de encontrar um algoritmo, mas quando os problemas foram propostos, não havia nenhuma noção matematicamente rigorosa para o conceito de algoritmo. Em uma linguagem mais atual: existe um algoritmo que, dada uma equação diofantina, determina se esta tem ou não solução?
Na proposta do décimo problema de Hilbert o foco de interesse aqui é apenas na existência das soluções e não na obtenção explícita destas soluções. Na conferência internacional de matemática de 1928, juntamente com seu orientado Wilhelm Ackermann (1896 – 1962), estabeleceu outras três influentes questões que tinham relação direta com o décimo problema 3:
- Seria a matemática completa, no sentido de que toda e qualquer afirmativa matemática possa ser sempre provada ou negada?
- Seria a matemática consistente, no sentido de que jamais se possa chegar a uma inconsistência por meio de raciocínio logicamente correto?
- Poderia a matemática decidir por si só, no sentido de que existe um procedimento mecânico capaz de determinar a falsidade ou a veracidade de qualquer afirmação?
Kurt Friedrich Gödel, já em 1931, trouxe contribuições respondendo negativamente às duas primeiras, ao provar que não é possível utilizar uma teoria matemática para demonstrar sua própria consistência e que dada uma teoria matemática, sempre existirão questões cujas as provas ou negações estarão fora do alcance daquela teoria. São teoremas que, de certa forma, estabelecem os limites da própria matemática, chamados de teoremas da incompletude de Gödel 4. Com palavras muito simples, pode-se dizer que estes teoremas afirmam que sempre existirão fatos verdadeiros que não podem ser matematicamente demonstrados.
Os problemas postulado por Hilbert precede invenção de computadores em décadas. Foi apenas nos anos 30 que tais questões foram formuladas e tratadas dentro do que ficou depois conhecido como teoria da computabilidade.
1.3 Máquina de Turing
Em 1936 Alan Mathison Turing (1912 - 1954) deu início à fundamentação das bases teóricas da ciência da computação, mostrando que era possível executar operações computacionais sobre a teoria dos números por meio de uma máquina que tivesse embutidas as regras de um sistema formal. Embora propriamente não existisse tal máquina, ele enfatizou desde o início que tais mecanismos poderiam ser construídos. Seu trabalho abriu uma nova perspectiva no esforço de formalizar a matemática e a computação.
Esta máquina hipotética ficou conhecida mais tarde como Máquina de Turing. Foi em um artigo intitulado “On Computable Numbers, with an application on the Entscheidungsproblem” que esta teoria foi estabelecida pela primeira vez, dando uma resposta ao 10o problema de Hilbert 5. Ao unir matemática e lógica na forma de uma máquina, Turing tornou possíveis sistemas processadores de símbolos. Hoje todos os computadores são construídos tendo como base o modelo da Máquina de Turing.
O processo computacional foi graficamente mostrado por Turing que considerou um dispositivo que pudesse ler e escrever símbolos em uma fita que estava dividida em quadrados. Uma cabeça de leitura e gravação se moveria em qualquer direção ao longo da fita, um quadrado por vez, e uma unidade de controle poderia interpretar uma lista de instruções simples sobre leitura e gravação de símbolos nos quadrados, movendo-se, ou não, para a direita ou esquerda. O quadrado que é lido em cada etapa é conhecido como “quadrado ativo”. A regra que está sendo executada determina o que se convencionou chamar estado da máquina. A fita é potencialmente infinita 6.
Fita Infinita

Esquema de uma Máquina de Turing
Cada instrução estabelece uma ação a ser executada. No caso, são estabelecidos quatro diferentes tipos de regra:
- Substituir branco por símbolo;
- Substituir símbolo por branco;
- Mover um quadrado para a direita;
- Mover um quadrado para a esquerda.
A máquina recebe um conjunto de instruções e executa. O dispositivo pode mover a cabeça de leitura e gravação para a direita ou esquerda, ler a posição, substituir um o branco por símbolo, símbolo por branco ou apenas mover a cabeça novamente.
1.4 Lei de Moore
No ano de 1965, Gordon Earl Moore (1929 - ), tornou-se cofundador e presidente da Intel e constatou que a complexidade para construção de componentes (transistores), a um custo mínimo, tem aumentado aproximadamente um fator a cada dois anos. Em outras palavras, o número de transistores dos chips tem um aumento de 100%, pelo mesmo custo, a cada período de 2 anos 7. Essa previsão ficou conhecida com a Lei de Moore que mais tarde foi revista para um período que seria a cada 18 meses.
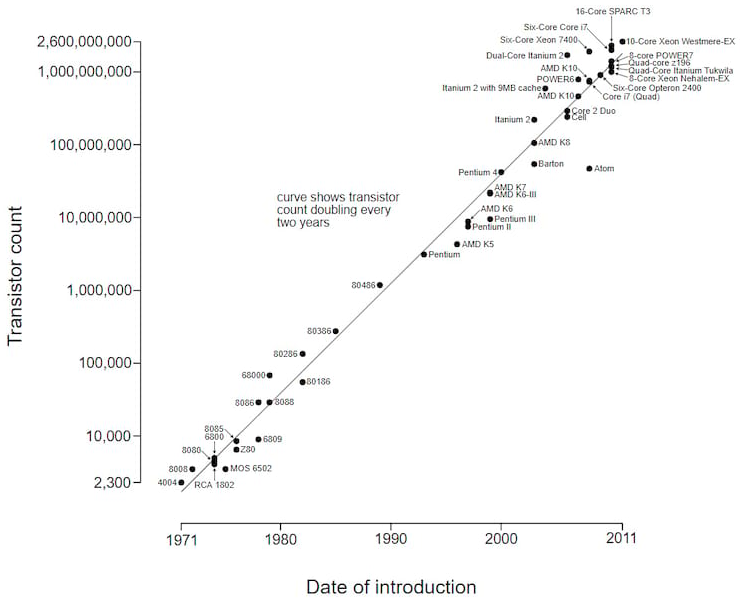
Microprocessor Transistor Counts 1971-2011 & Moore's Law
Uma das consequências da lei de Moore é a corrida das indústrias de semicondutores, que investiam significativamente seus recursos para seguir a previsão. Sem ela talvez não existisse um nível tão acelerado do desenvolvimento dos hardwares em um curto período.
1.5 Início da computação quântica
Pode-se considerar o marco inicial da computação quântica o ano de 1981 com o físico Richard Philips Feynman (1918 – 1988) elaborando a primeira proposta de um dispositivo que se utiliza de fenômenos quânticos para executar rotinas computacionais. Feynman argumentou que computadores clássicos podem simular a física clássica, porém o mesmo não ocorre com a física quântica, uma vez que a dimensão do espaço nela tratado, cresce exponencialmente em função do número de partículas acrescentadas ao sistema. Ele, então, questionou se um dispositivo que usasse as leis da mecânica quântica, para realizar cálculos, não poderia simular eficientemente a mecânica quântica 8.
Vale observar que é relativamente fácil modelar o comportamento de um átomo em um computador clássico, porém um gás em uma sala possui algo em torno de 10 elevado a 26 átomos, o que precisaria de algo em torno de bilhões e bilhões de gigabytes de memória para simular corretamente por vias clássicas 9.
1.6 Máquina de Turing quântica
Em 1985 David Deutsch (1953 - ) cria o primeiro algoritmo quântico e faz uma descrição do equivalente quântico para a máquina de turing 10. As funções realizadas em uma máquina de Turing Quântica ocorrem via interações quânticas. A fita e a cabeça em si existem em um estado quântico. No lugar da célula, a máquina de Turing Quântica abriga os q-bits, que apresentam estados de superposição de 0 ou 1. Ela pode codificar muitas entradas para um problema simultaneamente e calcular todas as entradas ao mesmo tempo.
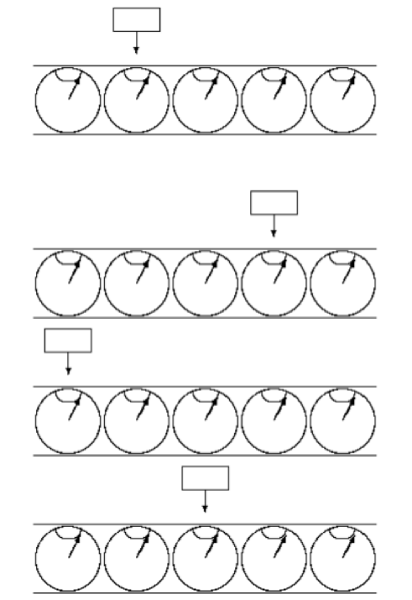
Esquema de uma Máquina de Turing Quântica
Observa-se na figura 1.3 o primeiro esquema representando o estado inicial da fita e da cabeça. Os desenhos seguintes representam as posições diferentes que a cabeça se movimentam, podendo apresentar um estado superposto desses três estados ao mesmo tempo.
1.7 Algoritmos quânticos
Em 1994 Peter Shor mostra que problemas considerados intratáveis por computadores clássicos, como a fatoração de números primos, podem ser resolvidos com computadores quânticos. Grande parte da ciência da computação é fundamentada na teoria dos números e as propriedades dos números primos. A segurança digital se baseia em códigos de criptografia, embasados na fatoração de números primos. Shor revoluciona o mundo da computação com o seu algoritmo, diminuindo o tempo de fatoração 11. Grover em 1996 demonstra, que em computação quântica, o tempo para se encontrar um elemento é substancialmente menor em relação à clássica 12.
1.7.1. O Algoritmo de Shor
Desde a proposição da computação quântica por Richard Feymann não houveram muitos avanços significativos na área até 1994. Nesse ano, o pesquisador Peter Shor, dos laboratórios da AT&T Bell escreveu um algoritmo que utiliza propriedades do computador quântico para realizar a fatoração de números inteiros grandes (na ordem de dígitos) em tempo polinomial. Esse algoritmo quântico, que ficou conhecido como algoritmo de Shor, foi publicado no artigo “Algorithms for Quantum Computation: Discrete Logarithms Factoring”.
O algoritmo utiliza justamente a propriedade da superposição quântica para conseguir reduzir, através de funções quânticas específicas, a complexidade do tempo de solução do problema de fatoração de exponencial para polinomial. O entendimento das funções quânticas que são utilizadas no algoritmo de Shor requer uma explicação matemática bastante extensa, que fogem do escopo desde texto. A aplicação imediata do algoritmo de Shor é na área de criptografia. A segurança dos sistemas de criptografia de chave pública baseia-se justamente na dificuldade de fatoração de números muito grandes; com a implementação prática de um computador que consiga realizar esses cálculos de forma rápida a segurança desses sistemas de criptografia estará comprometida. No entanto, conforme explicado a seguir, a tecnologia atual consegue construir computadores quânticos de apenas 7 qubits.
O problema da fatoração de números inteiros é muito utilizado na criptografia por acreditar-se que seja um problema difícil (exponencial). Contudo, Peter Shor causou surpresa ao descobrir um algoritmo que roda em tempo polinomial , onde é o número de bits do produto para realizar a fatoração de números inteiros. Isso significa que a construção de um computador quântico de tamanho suficiente irá tornar muitos algoritmos criptográficos, como o RSA, inseguros.
O algoritmo de Shor 11 se aproveita do fato que o problema da fatoração pode ser reduzido ao problema de encontrar o período de uma certa função. Para ilustrar, considere um número com e primos (pode-se generalizar para um número com qualquer quantidade de fatores). O problema de encontrar e dado é equivalente ao de encontrar o período da função com a relativamente primo a , pois pode-se mostrar que dividirá .
O algoritmo consiste em criar uma superposição quântica sobre todos os números , etc, e achar o período dessa sequência. Isso é realizado com a versão quântica da transformada discreta de Fourier. Com ela, obtém-se o período, e repetindo o processo com outros valores de , consegue-se informação suficiente para se descobrir e .
1.8 Desenvolvimento do hardware
Os primeiros protótipos de computador quântico apareceram em 1999 , no MIT (Massachusettes Institute of Technology). Em 2007, a empresa canadense D − Wave anunciou a construção do primeiro processador quântico do mundo, o Orion, com capacidade de processamento de 16 q-bits. Na sequência IBM e Google se adiantaram também no desenvolvimento.
Em novembro de 2017, a IBM anunciou sucesso no desenvolvimento de um computador quântico de 50 q-bits. E em janeiro de 2018, foi a vez da Intel (49 q-bits), e em março a Google (72 q-bits).

Computador quântico da canadense D-Wave
A capacidade computacional de um computador quântico pode ser impressionante, por exemplo, um processador de 100 q-bits seria mais poderoso do que a soma de todos os computadores atuais no planeta.
Nenhuma empresa propôs formalmente a entrada de seus computadores quânticos no mercado. A perspectiva é que os computadores quânticos entrem no mercado não para substituir completamente os PCs tradicionais, mas para integrá-los em um sistema mais poderoso.
Sua real eficácia foi comprovada recentemente pela IBM, mostrando que computadores quânticos são muito mais rápidos do que os modelos tradicionais na resolução de alguns problemas 13.
2. Computação Quântica
Um computador quântico executa cálculos utilizando-se das propriedades da mecânica quântica, e isso já muda o paradigma em relação a computação clássica drasticamente. Analogamente a um computador clássico, que funciona a partir de circuitos elétricos e portas lógicas manipulando bits, o computador quântico opera a partir de circuitos quânticos baseados em portas lógicas quânticas, manipulando a sua unidade fundamental, o q-bit.
Em um computador quântico a unidade básica de informação é o qubit (quantum bit). Um qubit pode assumir os valores de 0 ou 1, assim como um bit (binary digit) convencional. A diferença é que o qubit pode assumir ambos os valores de 0 ou 1 ao mesmo tempo! É nessa propriedade particular que está todo o poder computacional de um computador quântico. Apesar de ser pouco intuitivo (especialmente em uma cultura digital, onde tudo é exatamente 0 ou 1) e até mesmo contraditório com a física clássica, esse fenômeno quântico pode ser observado em laboratório, através de uma experiência conhecida como “divisão de raio”.
2.1. Dividindo o Fóton
Nessa experiência, uma fonte de luz é colocada em direção a uma lente. Adicionalmente, dois sensores óticos (A e B) são posicionados de tal forma de detectem as duas possíveis trajetórias do raio emitido pela fonte, conforme a figura abaixo. A fonte de luz emite um único fóton por vez, várias vezes. Sabe-se que um fóton é indivisível, ou seja, ele não pode ser particionado em duas unidades menores. Finalmente, a lente utilizada no experimento é tal que pode direcionar o fóton verticalmente, em direção ao sensor A, ou horizontalmente, em direção ao sensor B.
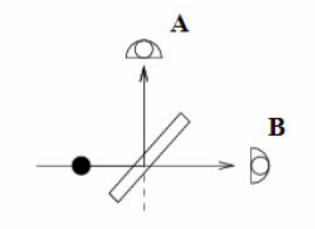
Dada a configuração do experimento, intuitivamente, espera-se que o fóton de luz emitido pela fonte seja refletido randomicamente pela lente e atinja um dos sensores óticos com a mesma probabilidade. De fato, esta experiência constata que o fóton é detectado em cada um dos sensores com a mesma probabilidade. Ou seja, em metade dos casos atinge o sensor A e, na outra metade, o sensor B. Até agora, a física clássica concorda com a física quântica.
Entretanto, a física quântica afirma que o fóton passa por ambas as trajetórias simultaneamente, todas as vezes! É aqui que a física quântica começa a diferenciar-se da física clássica e os conceitos ficam cada vez menos intuitivos. Para verificar essa afirmação é realizada uma nova experiência, onde dois espelhos e mais uma lente são acrescentados, conforme ilustrado na figura a seguir. A segunda lente utilizada é idêntica à primeira e os espelhos sempre refletem a luz na mesma direção.
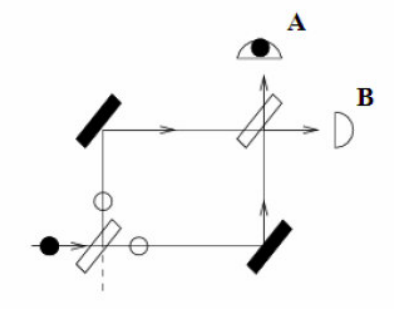
Nesta experiência, como na anterior, emite-se apenas 1 único fóton por vez, várias vezes. Entretanto, desta vez, verifica-se que apenas um dos sensores registra o fóton, todas as vezes. Ou seja, a probabilidade de que o fóton atinja um dos sensores (A ou B) é de 100% enquanto a do outro é nula. A explicação para esse fenômeno é que o fóton passa pelos dois caminhos possíveis simultaneamente, criando uma interferência no ponto de intersecção (a segunda lente), anulando a probabilidade do fóton alcançar o outro sensor. Esse efeito é chamado de single-particle interference.
Em outras palavras, isso quer dizer que tudo o que pode acontecer, de fato, acontece. Mas como isso pode acontecer se na primeira experiência o fóton era detectado em ambos os sensores com a mesma probabilidade? Eles não deveriam atingir os dois sensores em todos os casos? A resposta da física quântica é que quando observamos o sistema todas as possibilidades colapsam em uma única ocorrência em particular, que é a realidade tal qual a conhecemos (talvez seja dessa parte da física quântica que autores de ficção científica inspirem-se e imaginem universos paralelos!). Isso quer dizer que o simples ato de observar o sistema pode influenciá-lo, alterando o seu desfecho. Conforme será explanado adiante, essa é uma das principais dificuldades em construir um computador quântico.
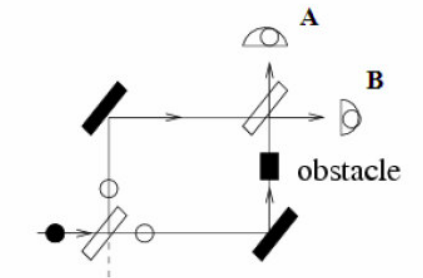
A única forma de observar que o fóton percorre as duas trajetórias ao mesmo tempo é através da interferência causada pela intersecção dos dois estados possíveis do sistema. Se for colocado um obstáculo sobre uma das trajetórias, conforme ilustrado pela figura a seguir, os sensores passam a registrar fótons como na primeira experiência, ou seja, com probabilidade de 0,5. Essa experiência demonstra o princípio básico da computação quântica e o enorme potencial para processamento paralelo de um computador quântico.
3. Bit quântico (q-bit)
A estrutura básica de informação na computação clássica é o bit, a estrutura análoga na computação quântica é o bit quântico, que é usualmente chamado de q-bit (qbit, qubit ou quibit). Um q-bit é um estado quântico da forma: , onde (números complexos), as amplitudes, com e é uma base que expande . Essa base é chamada de base computacional e pode ser representada por notação matricial como segue:
Quando sofre uma medição, o q-bit pode colapsar para o estado com probabilidade , ou para com probabilidade . O vetor é chamado de superposição dos vetores, com amplitudes e . Em mecânica quântica, o vetor é também chamado de estado 14.
A principal diferença, entre o bit clássico e o bit quântico, é que o bit clássico pode estar somente com um valor armazenado num determinado instante, esse valor é 0 ou 1. O bit quântico (q-bit) está numa sobreposição de 0’s e 1’s num determinado instante, ou seja, 0 e 1 estão armazenados ao mesmo tempo. Realizar uma medição de um sistema quântico é um problema central na teoria quântica, e muitos estudos foram e continuam sendo feitos nessa área. Em um computador clássico, é possível a princípio saber sobre o estado de qualquer bit em memória, sem alterar o sistema. No computador quântico, a situação é diferente, q-bits podem estar em estados sobrepostos, ou até mesmo emaranhados, e o simples ato de medir um estado quântico altera seu estado.
3.1. Esfera de bloch
COMING SOON:
4. Portas quânticas
Similar ao sistemas clássico de computação, as portas lógicas quânticas realizam a função de um operador lógico atuando na informação, ou nos q-bits, e assim manipulando ou alterando o seu estado
4.1 Portas quânticas de 1 q-bit
O conjunto de portas quânticas, matrizes de transformação, que realizam operações unitárias sobre um q-bit é infinito, pois as possibilidades de matrizes unitárias são infinitas. As matrizes unitárias garantem que a computação possa ser reversível.
Dado um q-bit em um estado arbitrário que passará pela porta quântica produzindo o resultado e a porta quântica inversa da no q-bit , tem como resultado o q-bit inicial .
Um vetor de estado (q-bit) deve ser unitário, e portanto, após a aplicação de uma porta quântica, tem-se outro vetor de estado que continuará sendo unitário 15.
Seguem algumas das portas mais usuais:
4.2. Portas quânticas de múltiplos q-bits
COMING SOON:
bits X qubits
Outra importante diferença entre os bits e os qubits é que qubits podem estar entrelaçados entre si. Sendo assim, de acordo com a quantidade de qubits entrelaçados e o modo como são usados, a computação quântica, quando comparada com a tradicional, pode atingir valores extraordinários:
- 1 qubit = 2 bits
- 2 qubits = 4 bits
- 3 qubits = 8 bits (1 byte)
- 4 qubits = 16 bits
- 13 qubits = 8.192 bits (1kb)
- 23 qubits = 8.388.608 bits (1mb)
- 33 qubits = 8.589.934.592 bits (1gb)
- 43 qubits = 8.796.093.022.208 bits (1 terabyte)
- n qubits = bits
Podendo ser exponencialmente mais poderosos que os bits tradicionais, os qubits abrem margem para vários problemas antes tidos como inviáveis computacionalmente. Em 1993, o estadunidense Peter Shor formulou um algoritmo quântico capaz de decompor um número com muitos algarismos em seus fatores primos, o qual foi nomeado como algoritmo de Shor. O ponto chave é que criptografias complexas, usadas na segurança dos nossos dados, são justamente baseadas nessa fatoração, visto que a quebra da criptografia seria inviável computacionalmente. Porém, essa não é uma realidade para computadores quânticos, que por meio do algoritmo de Shor conseguiriam quebrar uma criptografia em tempo polinomial em relação ao número de bits.
| Tamanho do número a ser fatorado em bits | Tempo de fatoração por Algorítimo Clássico | Tempo de fatoração por Algorítimo Quântico |
|---|---|---|
| 512 | 4 dias | 34 segundos |
| 1024 | 100 mil anos | 4,5 minutos |
| 2048 | 100 mil bilhões de anos | 36 minutos |
| 4096 | 100 bilhões de quatrilhões de anos | 4,8 horas |
Fonte: Revista Ciência Hoje, Vol. 33, n. 193, Maio de 2003.
Entretanto nem tudo está perdido, embora a criptografia atual esteja com seus dias contados, a computação quântica torna possível o surgimento de uma nova criptografia, a criptografia quântica. Muito mais segura que qualquer outro método de criptografia utilizado nas comunicações atuais, a criptografia quântica destaca-se por não necessitar de comunicações secretas prévias, como envio de chaves, pois a sua segurança se baseia em leis físicas. A maneira como essa criptografia é implementada diverge entre os existentes protocolos quânticos de comunicação, porém, a ideia principal é a utilização de um sistema físico entre os usuários do canal de comunicação, assim, caso algum intruso tente interceptá-lo, o estado quântico desse sistema será quebrado, tornando possível a identificação de uma invasão. Portanto, ainda que considerado um invasor com poder computacional ilimitado, essa criptografia permanece segura.
6. Conclusão
Para realizar a maioria dos cálculos matemáticos, editar textos ou navegar na Internet, os computadores atuais (baseados na arquitetura de Von Neumann) são a melhor solução. De fatos, os processadores atuais são extremamente eficientes para realizar essas tarefas. Entretanto, em áreas como a Inteligência Artificial, torna-se interessante a utilização de outros tipos de computadores e arquiteturas. Em algoritmos de reconhecimento de imagens ou processamento da fala, por exemplo, a execução sequencial e o armazenamento de dados da arquitetura de Von Neumann (que são tão eficientes para outras aplicações) tornam-se uma restrição que acaba limitando o desempenho desses sistemas. Para esse tipo de aplicação, torna-se mais interessante um tipo de computador que possua bastante poder de processamento paralelo para facilitar o reconhecimento de padrões (o princípio comum de solução desses problemas). Entre as diversas propostas alternativas, o computador quântico apresenta-se como a opção mais promissora, justamente porque a computação quântica é a que mais se diferencia da arquitetura de Von Neumann, com um poder de processamento paralelo maciço.
Portanto, o computador quântico não será utilizado para resolver os problemas que um computador clássico já resolve eficientemente. A computação quântica será aplicada em problemas que ainda não possuem solução eficiente, como a Inteligência Artificial e a Criptografia.
Este trabalho teve como principal escopo contribuir a compreensão a divulgação desse campo transversal às áreas da matemática, computação, física e engenharia, que é a computação quântica. A adoção do paradigma quântico na computação parece ser uma trajetória natural, e caminha concomitante com a diminuição do tamanho dos dispositivos eletrônicos presentes nos computadores, como já previa a Lei de Moore. Seria um erro pensar nela como mais uma dentre muitas tentativas de substituição de uma tecnologia em vias de esgotamento. O embasamento teórico necessário transita entre a matemática, em especial a álgebra linear no espaço dos complexos, e conceitos de física moderna. Essas compreensões são indispensáveis ao interessado na área.
Os circuitos quânticos são a forma mais simples para entender do funcionamento de computadores quânticos. A impossibilidade de construção de computadores quânticos em grandes escalas faz com que simulação deles em computadores clássicos seja valorosa, já que para desenvolver novos algoritmos quânticos é necessário também testá-los. Simuladores não devem apenas fornecer o resultado de cálculos, devem permitir a extração de informações importantes acerca de algoritmos simulados. Portanto, um bom simulador pode ser uma excelente ferramenta ao pesquisador.
Finalizando a segunda década do século XXI, a computação quântica e seus conceitos ainda são relativamente restritos e pouco divulgados. Espera-se que este texto contribua para que outros se interessem por esse campo da ciência. Não apenas a teoria, mas também as aplicações e a divulgação que incentivam o autor a continuar nesta área fascinante. O estudo de novos algoritmos quânticos, bem como a sua implementação, visando diversas áreas do conhecimento. Uma área, também interessante, seria a construção de novos simuladores.
6. Referências
-
P. Amiri. Quantum computers. Potentials, IEEE, 21(5):6–9, 2002. ↩
-
David Hilbert. Mathematical problems. international congress of mathematicians at paris in 1900. Translated by Mary Winston Newson, 1902. 2 ↩
-
David Hilbert e Wilhelm Ackermann. Principles of Mathematical Logic. Springer-Verlag, 1o edição, 1928. 2 ↩
-
Kurt Gödel. Über formal unentscheidbare sätze der principia mathematica und verwandter systeme, i. Monatshefte für Mathematik und Physik, 1931. 2 ↩
-
Allan Turing. On computable numbers with an application to the entscheidungsproblem. C. F. Hodgson and Son, 1936. 3 ↩
-
Michael Sipser. Introdução à Teoria da Computação. Cengage Learning, 2o edição, 2005. 3 ↩
-
Gordon E. Moore. Cramming more components onto integrated circuits. Electronics Magazine, 1965. ix, 4 ↩
-
Richard P. Faynman. Simulating physics with computers. International Journal of Theoretical Physics, 21(6/7), 1982. 5 ↩
-
Ivan S. Oliveira e Roberto S. Sarthour. Computação quântica e informação quântica. V Escola do CBPF, 2004. ix, xi, 5, 19, 20 ↩
-
David Deutsch. Quantum theory, the church-turing principle and the universal quantum computer. Proceedings of the Royal Society of London, 1985. 5, 32 ↩
-
Peter W. Shor. Algorithms for quantum computation: Discrete logarithms and factoring. Em 35th Annual Symposium on Foundations of Computer Science, 1994. 6 ↩ ↩2
-
Lov K. Grover. Fast quantum mechanical algorithm for database search. 28th Annual ACM Symposium on Theory of Computing, 1996. 6 ↩
-
Sergey Bravyi, David Gosset e Robert König. Quantum advantage with shallow circuits. Science, 2018. 6 ↩
-
Renato Portugal, Carlile C. L. e Luiz M. Carvalho end Nelson Maculan. Uma Introdução à Computação Quântica. SBMAC, 2o edição, 2012. 17 ↩
-
Michael A. Nielsen e Isaac L. Chuang. Quantum Computing and Quantum Information. Cambridge University Press, 1o edição, 2000. ix, xi, 8, 9, 11, 12, 21, 32, 36, 43, 44 ↩